问题
解答题
（2012•广东）设a＜1，集合A={x∈R|x＞0}，B={x∈R|2x2﹣3（1+a）x+6a＞0}，D=A∩B．
（1）求集合D（用区间表示）；
（2）求函数f（x）=2x3﹣3（1+a）x2+6ax在D内的极值点．
答案
（1）
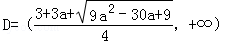
（2）见解析
（1）记h（x）=2x2﹣3（1+a）x+6a（a＜1）
△=9（1+a）2﹣48a=（3a﹣1）（3a﹣9）
当△＜0，即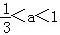
，D=（0，+∞）
当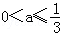
，
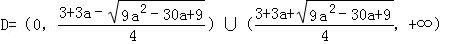
当a≤0，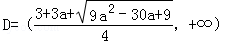
（2）由f'（x）=6x2﹣6（1+a）x+6a=0得x=1，a
①当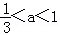
，f（x）在D内有一个极大值点a，有一个极小值点
②当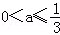
，∵h（1）=2﹣3（1+a）+6a=3a﹣1≤0
h（a）=2a2﹣3（1+a）a+6a=3a﹣a2＞0
∴1∉D，a∈D
∴f（x）在D内有一个极大值点a
③当a≤0，则a∉D
又∵h（1）=2﹣3（1+a）+6a=3a﹣1＜0
∴f（x）在D内有无极值点
