问题
问答题
如图所示,一固定的矩形导体线圈水平放置,线圈的两端接一只小灯泡,在线圈所在空间内存在着与线圈平面垂直的均匀分布的磁场.已知线圈的匝数n=100匝,总电阻r=1.0Ω,所围成矩形的面积S=0.040m2,小灯泡的电阻R=9.0Ω,磁感应强度随时间按如图乙所示的规律变化,线圈中产生的感应电动势瞬时值的表达式为e=nBmS
cos 2π T
t,其中Bm为磁感应强度的最大值,T为磁场变化的周期,不计灯丝电阻随温度的变化,求:2π T
(1)线圈中产生感应电动势的最大值;
(2)小灯泡消耗的电功率;
(3)在磁感应强度变化的0~
时间内,通过小灯泡的电荷量.T 4
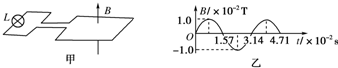
答案
(1)由图象知,线圈中产生的交变电流的周期T=3.14×10-2s,所以Em=nBmSω=
=8.0 V.2πnBmS T
(2)电流的最大值Im=
=0.80A,有效值I=Em R+r
=Im 2
A,则2 2 5
小灯泡消耗的电功率P=I2R=2.88W.
(3)在0~
时间内,根据法拉第电磁感应定律得,电动势的平均值T 4
=n. E
=n△Φ △t
,平均电流△Bs △t
=. I
=. E R+r nS△B (R+r)△t
流过灯泡的电荷量Q=
△t=. I nS△B R+r
代入解得Q=4.0×10-3C.
答:
(1)线圈中产生感应电动势的最大值为8V;
(2)小灯泡消耗的电功率为2.88W;
(3)在磁感应强度变化的0~
时间内,通过小灯泡的电荷量为4.0×10-3C.T 4
