问题
选择题
一个多边形的内角和与它的一个外角和为570°,则这个多边形的边数为( )
A.5
B.6
C.7
D.8
答案
答案:A
本题考查多边形的内角和与外角和、方程的思想.关键是记住内角和的公式与外角和的特征,还需要懂得挖掘此题隐含着边数为正整数这个条件.本题既可用整式方程求解,也可用不等式确定范围后求解.
解法1:设边数为n,这个外角为x度,则0<x<180°根据题意,得
(n-2)?180°+x=570°
解之,得n=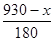 .
.
∵n为正整数,
∴930-x必为180的倍数,
又∵0<x<180,
∴n=5.
解法2:∵0<x<180.
∴570-180<570-x<570,即390<570-x<570.
又∵(n-2)?180°=570-x,
∴390<(n-2)?180°<570,
解之得4.2<n<5.2.
∵边数n为正整数,
∴n=5.
故选A.
此题较难,考查比较新颖,涉及到整式方程,不等式的应用.
