问题
问答题
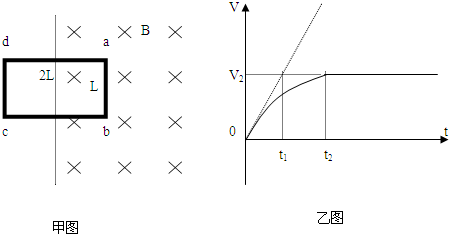
一有界磁场区域如图甲所示,质量为m、电阻为R的长方形矩形线圈abcd边长分别为L和2L,线圈一半在磁场内,一半在磁场外,磁感强度为B0.t0=0时刻磁场开始随时间均匀减小,线圈中产生感应电流,在磁场力作用下运动,V-t图象如图乙,图中斜向虚线为过0点速度图线的切线,所测数据t1、t2、V2 已由图中给出,不考虑重力影响.
求:(1)磁场磁感强度的变化率. (2)t2时刻后的回路电功率.
答案
(1)由v-t图可知道,刚开始t=0时刻线圈加速度为 a=
①v2 t1
此时感应电动势 E=
=△Φ △t
L2 ②△B △t
I=
=E R
?△B △t
③L2 R
线圈此刻所受安培力为 F=B0IL=
?B0L3 R
④△B △t
据牛顿第二定律得 F=ma ⑤
联立①④⑤
得到:
=△B △t mv2R B0t1L3
(2)线圈t2时刻开始做匀速直线运动,有两种可能:
(a)线圈没有完全进入磁场,磁场就消失,所以没有感应电流,回路电功率P=0.
(b)磁场没有消失,但线圈完全进入磁场,尽管有感应电流,所受合力为零,同样做匀速直线运动
P=
=E2 R
=(2L2?
)2△B △t R 4m2
Rv 22 B 20
L2t 21
答:
(1)磁场磁感强度的变化率为
;mv2R B0t1L3
(2)t2时刻后的回路电功率为
.4m2
Rv 22 B 20
L2t 21
