问题
解答题
一个两位数，它的十位数字为a，个位数字为b，若把它的十位数字与个位数字对调，得到一个新的两位数．
①试计算新的两位数与原数的和与差；
②回答：这个和能被11整除吗？差呢？
答案
解：（1）（10b+a）+（10a+b）=10b+a+10a+b=11a+11b=11（a+b）；（10b+a）﹣（10a+b）=10b+a﹣10a﹣b=9b﹣9a=9（b﹣a）；
即新的两位数与原数的和为11（a+b），差为9（b﹣a）；
（2）这个和能被11整除，差不能被11整除．
∵和为和为11（a+b）
∴11（a+b）÷11=a+b所以这个和能被11整除；
差为9（b﹣a）9（b﹣a）÷11=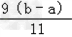
，b﹣a＜11
∴差不能被11整除．