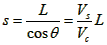问题
计算题
一条宽度为L的河流,水流速度为Vs,已知船在静水中的速度为Vc,那么:
(1)怎样渡河时间最短?
(2)若Vc>Vs,怎样渡河位移最小?
(3)若Vc<Vs,怎样渡河船漂下的距离最短?船渡河的最短位移是多少?
答案
解:(1)如图甲所示
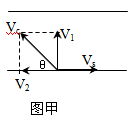
设船上头斜向上游与河岸成任意角θ,这时船速在垂直于河岸方向的速度分量V1=Vcsinθ,
渡河所需时间为: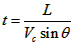
可以看出:L、Vc一定时,t随sinθ增大而减小;
当θ=900时,sinθ=1,所以当船头与河岸垂直时,渡河时间最短,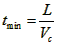
(2)如图乙所示,
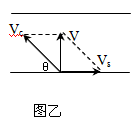
渡河的最小位移即河的宽度。为了使渡河位移等于L,必须使船的合速度V的方向与河岸垂直。
这是船头应指向河的上游,并与河岸成一定的角度θ。根据三角函数关系有:
Vccosθ─Vs=0,所以θ=arccosVs/Vc
因为0≤cosθ≤1,
所以只有在Vc>Vs时,船才有可能垂直于河岸横渡。
(3)如果水流速度大于船上在静水中的航行速度,则不论船的航向如何,总是被水冲向下游。
怎样才能使漂下的距离最短呢?如图丙所示,
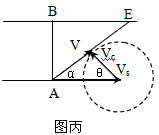
设船头Vc与河岸上游成θ角,合速度V与河岸下游成α角。
可以看出:α角越大,船漂下的距离x越短,那么在什么条件下α角最大呢?
以Vs的矢尖为圆心,以Vc为半径画圆,当V与圆相切时,α角最大,
根据cosθ=Vc/Vs,
船头与河岸的夹角应为:θ=arccosVc/Vs。
此时渡河的最短位移为: