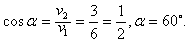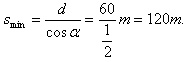问题
计算题
河宽60 m,水流速度v1=6m/s,小船在静水中速度v2=3 m/s,则:
(1)它渡河的最短时间是多少?
(2)最短航程是多少?
答案
解:(1)以水流速度方向为x轴正方向,以垂直对岸方向为y轴正方向,以船开出点为坐标原点建立坐标系,该船与岸成θ角开出(如图所示),将v2沿x、y方向分解,则

v2x=v2cosθ,v2y=v2sinθ
所以过河时间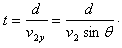
当θ=90°时过河的时间最短,且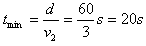
(2)先作出OA表示水流速度v1,然后以A为圆心以船在静水的速度v2的大小为半径作圆,过O作圆A的切线OB与圆A相切于B,连接AB,过O作AB的平行线,过B作OA的平行线,两平行线相交于C,则OC为船对水的速度v2(如图所示),由图不难看出,船沿OBD行驶到对岸位移最短,设v2与河岸的夹角为α,则有