问题
计算题
真空中存在空间范围足够大的、水平向右的匀强电场。在电场中，若将一个质量为m、带正电的小球由静止释放，运动中小球速度与竖直方向夹角为37°（取sin37°＝0.6，cos37°=0.8）。现将该小球从电场中某点以初速度v0竖直向上抛出。求运动过程中
（1）小球受到的电场力的大小及方向；
（2）小球从抛出点至最高点的电势能变化量；
（3）小球的最小动量的大小及方向。
答案
解：（1）根据题设条件，电场力大小Fe=mgtan37°＝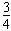
mg，电场力的方向水平向右
（2）小球沿竖直方向做匀减速运动，速度为v，vy=v0－gt
沿水平方向做初速度为0的匀加速运动，加速度为a，ax=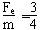
g
小球上升到最高点的时间t=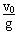
此过程小球沿电场方向位移sx=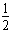
axt2=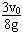
电场力做功W=Fxsx＝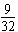
mv02
小球上升到最高点的过程中，电势能减少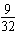
mv02
（3）水平速度vx=axt
竖直速度vy=v0－gt
小球的速度v=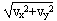
由以上各式得出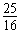
g2t2－2v0gt+(v02－v2)=0
解得当t=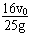
时，v有最小值vmin=
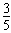v0
此时vx＝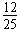
v0，vy=
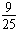v0，tanθ=
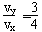，即与电场方向夹角为37°斜向上
小球动量的最小值为pmin=mvmin＝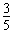
mv0
最小动量的方向与电场方向夹角为37°，斜向上