问题
选择题
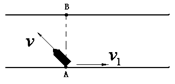
有一条河,河流的水速为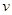 1,现有一条小船沿垂直于河岸的方向从A渡河至对岸的B点,它在静止水中航行速度
1,现有一条小船沿垂直于河岸的方向从A渡河至对岸的B点,它在静止水中航行速度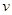 大小一定,当船行驶到河中心时,河水流速变为
大小一定,当船行驶到河中心时,河水流速变为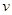 2(
2(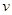 2>
2>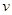 1),若船头朝向不变,这将使得该船
1),若船头朝向不变,这将使得该船
A.渡河时间增大
B.到达对岸时的速度增大
C.渡河通过的路程增大
D.渡河通过的路程比位移大
答案
BCD
分析:船航行时速度为静水中的速度与河水流速二者合速度,由运动的等时性知分析过河时间时,只分析垂直河岸方向的速度即可.当水流的速度变化时,船的合速度变化,那么合位移变化,因此到达对岸的地点变化.
解答:解:因为分运动具有等时性,所以分析过河时间时,只分析垂直河岸方向的速度即可,渡河时小船船头垂直指向河岸,即静水中的速度方向指向河岸,而其大小不变,因此,小船渡河时间不变,∴A选项错误.
当水流速度突然增大时,由矢量合成的平行四边形法则知船的合速度增大,即到达对岸时的速度增大,故B正确
当水流速度突然增大时,由矢量合成的平行四边形法则知船的合速度变化,因而小船到达对岸地点变化,在B点右边靠岸,所以渡河通过的路程增大,∴C选项正确.
由于河水流速增大,所以小船做折线运动,则渡河通过的路程比位移大,∴D选项正确.
故选:BCD.
点评:小船过河问题属于运动的合成问题,要明确分运动的等时性、独立性,运用分解的思想,看过河时间只分析垂直河岸的速度,船航行时速度为静水中的速度与河水流速二者合速度,使用平行四边形法则求合速度,水流速度变,则合速度变,过河位移变化.
