问题
问答题
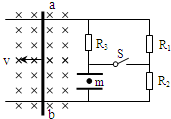
平行光滑导轨置于匀强磁场中,磁感应强度为B=0.4T,方向垂直于导轨平面.金属棒ab以速度v向左匀速运动.导轨宽度L=1m,电阻R1=R3=8Ω,R2=4Ω,导轨电阻不计(金属棒ab电阻不能忽略),平行板电容器两板水平放置,板间距离d=10mm,内有一质量为m=1×10-14㎏,电量q=1×10-15C的粒子,在电键s断开时粒子处于静止状态,s闭合后粒子以a=6m/s2的加速度匀加速下落,g取10m/s2.
求:(1)金属棒运动的速度为多少?
(2)s闭合后,作用于棒的外界拉力的功率为多少?
答案
(1)S断开时,粒子在重力与电场力作用下处于静止状态,得:mg=qE=
①qU1 d
S闭合时,粒子在重力和电场力作用下产生加速度,由牛顿第二定律得,mg-
=ma②qU2 d
代人数据解得,U1-U2=1.0V
开关闭合后,R1和R3并联总电阻R并=4Ω
闭合电路总电阻R=R2+R并=8Ω
根据串联电路的电压分配关系得:
=U2 R2 U1 R
代人数据解得:U1=2.0V
金属棒运动产生感应电动势
E=BLv=U1
所以:v=5.0m/s
(2)开关闭合后电路中的总电流:I=
=0.25AE R
作用与导体棒上的拉力:F=BIL=0.1N
作用于棒的外界拉力的功率为:P=Fv=0.5W
答:(1)金属棒运动的速度为5.0m/s;
(2)s闭合后,作用于棒的外界拉力的功率为0.5W.
