问题
解答题
已知集合A={x||x-1|≤1},B={x|x2-4ax+3a2≤0,a≥0}
(1)当a=1时,求集合A∩B;
(2)若A∩B=B,求实数a的取值范围.
答案
(1)由|x-1|≤1,即-1≤x-1≤1,
解得0≤x≤2,
∴A=[0,2],
当a=1时,B={x|x2-4x+3≤0}={x|1≤x≤3},
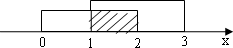
结合数轴,可知A∩B=[1,2];
(2)∵x2-4ax+3a2≤0,即(x-a)(x-3a)≤0,
又∵a≥0,
∴B={x|a≤x≤3a}
∵A∩B=B,
∴B⊆A,
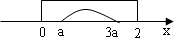
结合数轴可得,
,解得a∈[0,a≥0 3a≤2
],2 3
故实数a的取值范围为a∈[0,
].2 3
