问题
解答题
已知平面上的线段l及点P,任取l上一点Q,线段PQ长度的最小值称为点P到线段l的距离,记作d(P,l),
(1)求点P(1,1)到线段l:x-y-3=0(3≤x≤5)的距离d(P,l);
(2)设l是长为2的线段,求点的集合D={P|d(P,l)≤1}所表示的图形面积;
(3)写出到两条线段l1,l2距离相等的点的集合Ω={P|d(P,l1)=d(P,l2)},其中l1=AB,l2=CD,A,B,C,D是下 * * 组点中的一组.对于下 * * 种情形,只需选做一种.
①A(1,3),B(1,0),C(-1,3),D(-1,0)
②A(1,3),B(1,0),C(-1,3),D(-1,-2)
③A(0,1),B(0,0),C(0,0),D(2,0)
答案
解:(1)设 是线段
是线段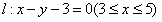 上一点,则
上一点,则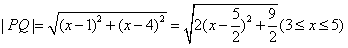
当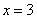 时,
时, ;
;
(2)设线段l的端点分别为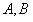 ,以直线
,以直线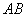 为x轴,
为x轴,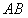 的中点为原点建立直角坐标系,则
的中点为原点建立直角坐标系,则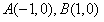 ,点集D由如下曲线围成
,点集D由如下曲线围成
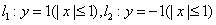
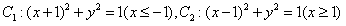
其面积为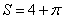 :
:
(3)① 选择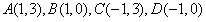 ,
,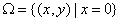
② 选择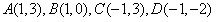
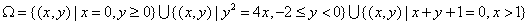
③ 选择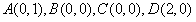
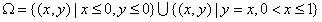
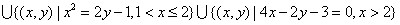 。
。
