问题
解答题
设关于x的方程(m+1)x2-mx+m-1=0有实根时,实数m的取值范围是集合A,函数f(x)=lg[x2-(a+2)x+2a]的定义域是集合B。
(1)求集合A;
(2)若A∪B=B,求实数a的取值范围.
答案
解:(1)当m+1=0,即m=-1时,方程为x-2=0,此时x=2,
当m+1≠0,即m≠-1时,
方程有实根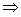 △=m2-4(m+1)(m-1)≥0,
△=m2-4(m+1)(m-1)≥0,
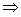 m2-4m2+4≥0
m2-4m2+4≥0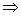 3m2≤4
3m2≤4
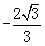 ≤m≤
≤m≤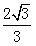 且m≠-1,
且m≠-1,
由上可知: 。
。
(2)∵A∪B=B,∴A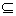 B,
B,
而B={x|x2-(a+2)x+2a>0}={x|(x-2)(x-a)>0},
当a>2时,B={x|x>a或x<2},
此时A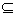 B,∴a>2适合;
B,∴a>2适合;
当a=2时,B={x|x≠2},此时A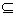 B,∴a=2也适合;
B,∴a=2也适合;
当a<2时,B={x|x>2或x<a},要使A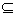 B,只要
B,只要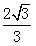 <a≤2;
<a≤2;
由此可知:a>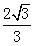 。
。

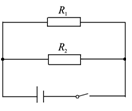
 车前排座位中安装有高低档的电加热,其工作原理相当于如图所示的电路图,其中R1=12 Ω,R2=6 Ω,闭合开关后,通过R1的电流为2 A.
车前排座位中安装有高低档的电加热,其工作原理相当于如图所示的电路图,其中R1=12 Ω,R2=6 Ω,闭合开关后,通过R1的电流为2 A. 电压;
电压;