问题
单项选择题
以下四个命题,不正确的是( ).
A.设
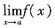 存在,则
存在,则
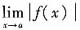 一定存在
一定存在
B.设
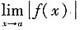 存在,则
存在,则
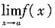 一定存在
一定存在
C.设|f(x)|在x=x0点处可导,则f(x)在x=x0点处不一定可导
D.设|f(x)|在x=x0点处连续,则f(x)在x=x0点处不一定连续
答案
参考答案:B
解析:本题是一元微积分的基本概念题.对于容易混淆的问题,考生在最后复习阶段,要好好总结和整理,一般说来,正确的要会证明,错误的要能举出反例.这种训练是有益的.
对于选项(A),事实上有如下结论:设[*],则[*].可以证明如下.[*]=[*],当0<|x-a|<δ时,|f(x)-A|<ε,又由于||f(x)|-|A||≤|f(x)-A|,故||f(x)|-|A||<ε,[*].命题正确,排除.
对于选项(B),反例f(x)=sgn(x),[*]不存在.命题错误,入选.
对于选项(C),反例-[*]在x=x0氧处不可导,|f(x)|在x=x0点处可导.命题正确,排除.
对于选项(D),[*]在x=x0点处不连续,|f(x)|在x=x0点处连续.命题正确,排除.
