问题
单项选择题
已知y=y(x)是微分方程(x2+y2)dy=dx-dy的任意解,则( ).
A.
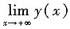 存在,
存在,
 不存在
不存在
B.
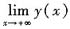 不存在,
不存在,
 存在
存在
C.
 不存在,
不存在,
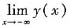 不存在
不存在
D.
 存在,
存在,
 存在
存在
答案
参考答案:D
解析:本题以微分方程的概念为载体,考查一元微积分学的综合知识,是一道有一定难度的综合题.
将微分方程(x2+y2)dy=dx-dy变形为[*],于是[*],则y=y(x)为严格单调增函数,根据单调有界准则,只要证明y(x)有界即可.
对[*]两边从x0到x积分,得[*],于是
[*]
设x≥x0,则[*]
[*]
y(x)有上界,所以[*]存在.
同理可证,当x≤x0时y(x)有下界,所以[*]也存在.故[*]存在,[*]也存在,答案选择(D).
