问题
解答题
如下数表是由从1开始的连续自然数组成，观察规律并完成各题的解答．
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36
…………………………
（1）表中第8行的最后一个数是______________，它是自然数_____________的平方，第8行共有____________个数；
（2）用含n的代数式表示：第n行的第一个数是___________________，最后一个数是
________________，第n行共有_______________个数；
（3）求第n行各数之和．
答案
略解：(1)64，8，15；
（2）n2-2n+2，n2，(2n-1);
（3）第n行各数之和：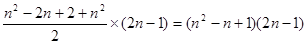
（1）观察数表可知，表中第8行的最后一个数是64，它是自然数8的平方，第8行共有15个数，故答案为：64，8，15；
（2）由（1）得出一般规律：第n行的第一个数是（n-1）2+1，最后一个数是n2，第n行共2n-1个数，
故答案为：（n-1）2+1，n2，2n-1；
（3）第n行第一个数为（n-1）2+1，最后一个为n2 总共2n-1个数
所以第n行各数之和=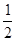
[（n-1）2+1+n2]×（2n-1）=（n2-n+1）（2n-1）