3

（1）根据已知条件a，b的符号，然后去绝对值即可得出结果，

（2）根据已知条件确定a，b，c，d之间的关系，然后利用|a-c|=|b-c|=|d-b|=1得出|a-d|的值．

（1）解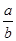：∵＞0，

∴a，b同号，

又∵a＜-b，即a+b＜0，

∴a，b必须同为负，

∴|a|-|b|+|a+b|+|ab|=-a-（-b）-（a+b）+ab=-2a+ab；

（2）解：已知b≠c，可设b＜c，

∵|a-c|=|b-c|，

∴a-c与b-c必互为相反数（否则a=b，不合题意），即a-c=-（b-c），a+b=2c，

又∵b＜c，

∴a＞c．

∵|b-c|=|d-b|，

∴b-c与d-b必相等（否则c=d，不合题意），即b-c=d-b，从而得2b=c+d，

∵b＜c，

∴b＞d，

即d＜b＜c＜a．

∴|a-d|=a-d=（a-c）+（c-b）+（b-d）=1+1+1=3．

若设b＞c，同理可得|a-d|=3．

本题主要考查了根据已知条件确定符号及去绝对值的运算，难度适中．