问题
解答题
已知：AOB为一直线，O在AB上，OE⊥OF，求证：∠1和∠2互余．
答案
证明：∵AOB为一直线，
∴∠1+∠2+∠FOE=180°，
∵OE⊥OF，
∴∠EOF=90°，
∴∠1+∠2=180°-90°=90°，
∴∠1和∠2互余．
搜题请搜索小程序“爱下问搜题”
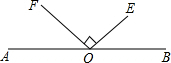
已知：AOB为一直线，O在AB上，OE⊥OF，求证：∠1和∠2互余．
证明：∵AOB为一直线，
∴∠1+∠2+∠FOE=180°，
∵OE⊥OF，
∴∠EOF=90°，
∴∠1+∠2=180°-90°=90°，
∴∠1和∠2互余．