问题
填空题
一动点P从数轴上表示―2的点A 1开始移动,第一次先向左移动1个单位,再向右移动2个单位到达点A 2;第二次从点A 2向左移动3个单位,再向右移动4个单位到达点A 3;第三次从点A 3向左移动5个单位,再向右移动6个单位到达点A 4,…...,点P按此规律移动,那么:(1)第一次移动后这个点P在数轴上表示的数是 ;
(2)这个点P移动到点A n时,点A n在数轴上表示的数是 .
答案
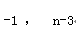
答案应为:-1; n-2.
根据数轴上的点的坐标向右为加,向左为减的特点可分别求出第一次、第二次、第三次移动后这个点在数轴上表示的数,找出规律即可求出第n次移动结果这个点在数轴上表示的数;
解:(1)第一次移动后这个点在数轴上表示的数:-2-1+2=-1;
(2)当n为奇数时,它在数轴上表示的数为:
-2-1+2-3+4-…-(n-2)+(n-1)-n=n-2(4分)
当n为偶数时,它在数轴上表示的数为:
-2-1+2-3+4-…-(n-1)+n=n-2.
故答案为:-1; n-2.
考查了数轴的知识,要注意数轴上点的移动规律是“左减右加”.把数和点对应起来,也就是把“数”和“形”结合起来,二者互相补充,相辅相成,把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的数学思想.
