问题
填空题
设x1,x2,x3,x4,x5,x6,x7是自然数,且x1<x2<x3<x4<x5<x6<x7,x1+x2=x3,x2+x3=x4,x3+x4=x5,x4+x5=x6,x5+x6=x7,又x1+x2+x3+x4+x5+x6+x7=2010,那么x1+x2+x3的值最大是 。
答案
236
不定方程的思想结合x1+x2+x3+x4+x5+x6+x7=13x1+20x2=2010,可得x1必是10的奇数倍,然后根据x1<x2可得出答案
解:∵x1+x2+x3+x4+x5+x6+x7=13x1+20x2=2010,
利用整除性,x1必是10的奇数倍,又x1<x2,
可得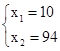
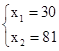 ,
,
(x1+x2+x3)max=2(x1+x2)max=2(50+68)=236.
故答案为:236
