问题
解答题
试举反例说明下列命题是假命题
小题1:如果a+b>0,那么ab>0:
小题2:如果a是无理数，b是无理数，那么a+b是无理数。
答案
小题1:反例：如a=3，b=-2；
a+b=3+(-2)=1>0.ab=3×（-2）＝-6<0
所以 原命题是假命题。……………………5分
小题2:反例：如a=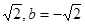
；
a+b=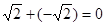
是有理数。
所以 原命题是假命题。……………………5分
（1）可以假设a=3，b=-2，a，b的和符合题设，但不符合结论，推出原命题为假命题，（2）举出符合题设的a，b的值，通过求和，结果并不符合结论，故推翻题设，推出原命题为假命题．
解：（1）反例：如a=3，b=-2；
∴a+b=3+（-2）=1＞0，
∴ab=3×（-2）=-6＜0，
∴原命题是假命题，
（2）反例：如a=；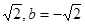
∴a+b=，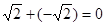
∵0是有理数，
∴原命题是假命题．