问题
单项选择题
已知ab≠1，且满足2a2+2008a+3=0和3b2+2008b+2=0，则（）。
A．3a-2b=0
B．2a-3b=0
C．3a+2b=0
D．2a+3b=0
答案
参考答案：B
解析：
方法一
2a2+2008a+3=0
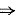4a2+2008×2a+6=0 ①
3b2+2008b+2=0
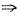9b2+2008×3b+6=0 ②
式①-②得
(2a-3b)(2a+3b)+2008(2a-3b)=0(2a-3b)(2a+3b+2008)=0
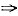2a-3b=0或2a+36+2008=0．
方法二 由于
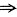，且ab≠1，所以
当
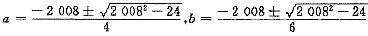时，
，
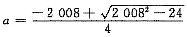当时，从而有2a-3b=0．选(B)．
或根据4a2-9b2+2008(2a-3b)=0，也可以推出有2a-3b=0．