问题
单项选择题
设矩阵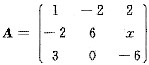 ,三阶矩阵B≠0,且满足AB=0,则()。
,三阶矩阵B≠0,且满足AB=0,则()。
A.x=-8,B的秩=1
B.x=-8,B的秩=2
C.x=8,B的秩=1
D.x=8,B的秩=2
答案
参考答案:A
解析:
方法一 由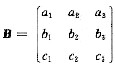 ,因AB=0,B≠0,故有即
,因AB=0,B≠0,故有即
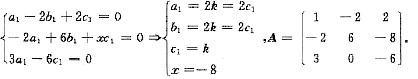 故可令
故可令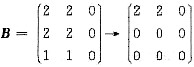 ,r(B)=1,选(A). 方法二 根据题意可知AX=0有非零解,所以
,r(B)=1,选(A). 方法二 根据题意可知AX=0有非零解,所以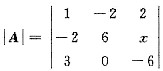 =-48-6x=0,故x=8.又由于r(A)=2,且B≠0,所以B的秩=1.选(A).
=-48-6x=0,故x=8.又由于r(A)=2,且B≠0,所以B的秩=1.选(A).
设矩阵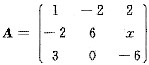 ,三阶矩阵B≠0,且满足AB=0,则()。
,三阶矩阵B≠0,且满足AB=0,则()。
A.x=-8,B的秩=1
B.x=-8,B的秩=2
C.x=8,B的秩=1
D.x=8,B的秩=2
参考答案:A
解析:
方法一 由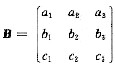 ,因AB=0,B≠0,故有即
,因AB=0,B≠0,故有即
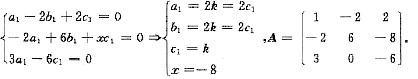 故可令
故可令 ,r(B)=1,选(A). 方法二 根据题意可知AX=0有非零解,所以
,r(B)=1,选(A). 方法二 根据题意可知AX=0有非零解,所以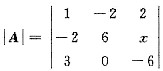 =-48-6x=0,故x=8.又由于r(A)=2,且B≠0,所以B的秩=1.选(A).
=-48-6x=0,故x=8.又由于r(A)=2,且B≠0,所以B的秩=1.选(A).