问题
单项选择题
若向量α，β，γ线性无关，而向量α+2β，2β+kγ，3γ+α线性相关，则k=（）。
A．3
B．2
C．-2
D．-3
答案
参考答案：D
解析：
因为向量α+2β，2β+kγ，3γ+α线性相关，所以存在不全为零的k1，k2，k3使得k1(α+2β)+k2(2β+kγ)+k3(3γ+α)=0，
即(k1+k3)α+(2k2+2k2)β+(kk2+3k3)γ=0，又向量α，β，γ线性无关，故
由非零解，从而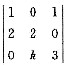
=6+2k=0，即k=-3．选(D)．