函数y=x2-4x+5（0≤x≤5）的最小值和最大值分别是______，______．
函数y=x2-4x+5的顶点坐标为：x=-
=-b 2a
=2，y=-4 2
=4ac-b2 4a
=1，即（2，1）．4×5-(4)2 4
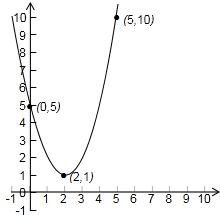
x=0时，y=02-4×0+5=5，即（0，5）；
x=5时，y=52-4×5+5=10，即（5，10）．
由函数y=x2-4x+5的图象可知，在0≤x≤5范围内，函数最小值和最大值分别是1，10．
2010年，我国货物进出口总额29728亿美元，比上年增长21.5%。其中，货物出口15780亿美元，比上年增长18.4%；货物进口13948亿美元，比上年增长25.6%。
| 2010年我国对主要国家和地区货物进出口额及其增长速度 单位：亿美元 | ||||
| 国家和地区 | 出口额 | 比上年增长(%) | 进口额 | 比上年增长(%) |
| 欧盟 美国 中国香港 东盟 日本 韩国 印度 中国台湾 俄罗斯 | 3112 2833 2183 1382 1211 688 409 297 296 | 31.8 28.3 31.3 30.1 23.7 28.1 38.0 44.8 69.0 | 1685 1020 123 1546 1767 1384 208 1157 258 | 31.9 31.7 40.9 44.8 35.0 35.0 51.8 35.0 21.7 |
2009年，我国货物进出口总额约为______亿美元。
A．20483
B．24467
C．27305
D．19689
