问题
解答题
已知二次函数y=x2-x-2及实数a>-2,求
(1)函数在一2<x≤a的最小值;
(2)函数在a≤x≤a+2的最小值.
答案
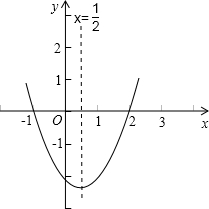
二次函数y=x2-x-2=(x-
)2-1 2
的图象如图:9 4
顶点坐标为(
,-1 2
),9 4
(1)当-2<a<
时,函数为减函数,1 2
最小值为当x=a时,y=a2-a-2.
当a≥
时,ymin=-1 2
,9 4
(2)当a>-2,且a+2<
,1 2
即:-2<a<-
时,函数为减函数,3 2
最小值为:yx=a+2=(a+2)2-(a+2)-2,
当a<
≤a+2,即-1 2
≤a<3 2
时,1 2
函数的最小值为y=-
.9 4