问题
解答题
函数y=ax2(a≠0)的图象与直线y=2x-3交于点(1,b).
(1)求a和b的值.
(2)求抛物线y=ax2的解析式,并求出顶点坐标和对称轴.
(3)x取何值时,二次函数y=ax2中的y随x的增大而增大?
(4)求抛物线与直线y=-2的两个交点及顶点所构成的三角形的面积.
答案
(1)把点(1,b)代入y=2x-3得2-3=b,解得b-=1,
所以交点坐标为(1,-1),
把(1,-1)代入y=ax2得-1=a,即a=-1;
(2)当a=-1时,二次函数解析式为y=-x2,
所以抛物线的对称轴为y轴,顶点坐标为(0,0);
(3)二次函数y=-x2,当x<0时,y随x的增大而增大;
(4)如图,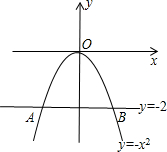 解方程组
解方程组y=-x2 y=-2
或x=- 2 y=-2
,x= 2 y=-2
所以A点坐标为(-
,-2),B点坐标为(2
,-2),2
所以S△OAB=
×2×21 2
=22
.2
