问题
解答题
已知集合A={x|mx2-2x+3=0，m∈R}.
（1）若A是空集，求m的取值范围；
（2）若A中只有一个元素，求m的值；
（3）若A中至多只有一个元素，求m的取值范围.
答案
(1) m＞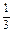
(2) m=0或m= 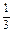（3）m=0或m≥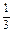
集合A是方程mx2-2x+3=0在实数范围内的解集.
（1）∵A是空集，∴方程mx2-2x+3=0无解.∴Δ=4-12m＜0,即m＞.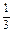
（2）∵A中只有一个元素，∴方程mx2-2x+3=0只有一个解.
若m=0，方程为-2x+3=0，只有一解x=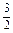
;若m≠0，则Δ=0，即4-12m=0,m=.
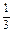∴m=0或m=.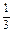
(3)A中至多只有一个元素包含A中只有一个元素和A是空集两种含义，根据（1）、（2）的结果，得m=0或m≥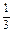.