问题
选择题
对于非空实数集A,记A*={y|∀x∈A,y≥x}.设非空实数集合M、P满足:M⊆P,且若x>1,则x∉P.现给出以下命题:
①对于任意给定符合题设条件的集合M、P,必有P*⊆M*;
②对于任意给定符合题设条件的集合M、P,必有M*∩P≠∅;
③对于任意给定符合题设条件的集合M、P,必有M∩P*=∅;
④对于任意给定符合题设条件的集合M、P,必存在常数a,使得对任意的b∈M*,恒有a+b∈P*.其中正确的命题是( )
A.①③
B.③④
C.①④
D.②③
答案
答案:C
对于②,假设M=P=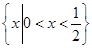 ,则M*=
,则M*= ,则M*∩P=∅,因此②错误;对于③,假设M=P=
,则M*∩P=∅,因此②错误;对于③,假设M=P=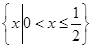 ,则
,则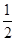 ∈M,又
∈M,又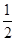 ∈P*,则M∩P*≠∅,因此③也错误,而①和④都是正确的,故选C.
∈P*,则M∩P*≠∅,因此③也错误,而①和④都是正确的,故选C.
