问题
解答题
抛物线的顶点在原点,以x轴为对称轴,经过焦点且倾斜角为135°的直线被抛物线所截得的弦长为8,试求抛物线方程.
答案
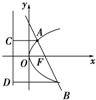
如图所示,依题意,设抛物线方程为y2=2px,则直线方程为y=-x+
p.设直线交抛物线于A(x1,y1)、B(x2,y2)两点,过A、B分别作准线的垂线,垂足分别为C、D.1 2
则由抛物线定义得|AB|=|AF|+|FB|=|AC|+|BD|
=x1+
+x2+p 2
,(4分)p 2
即x1+
+x2+p 2
=8.①p 2
又A(x1,y1)、B(x2,y2)是抛物线和直线的交点,
由
消去y,得x2-3px+y=-x+
p1 2 y2=2px
=0,p2 4
∵△=9p2-4×
=8p2>0.p2 4
∴x1+x2=3p.
将其代入①得p=2,
∴所求抛物线方程为y2=4x.
当抛物线方程设为y2=-2px(p>0)时,
同理可求得抛物线方程为y2=-4x.
故所求抛物线方程为y2=4x或y2=-4x.(8分)