问题
解答题
已知实数x，y满足：x2+3y2﹣3=0，求x+y的取值范围．
答案
解：已知等式x2+3y2﹣3=0可化为：
=1，
此为椭圆方程，故由椭圆的参数方程可知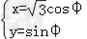
（φ为参数）
所以x+y=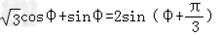
，
故由三角函数的性质，可知x+y的取值范围为[﹣2，2]．
搜题请搜索小程序“爱下问搜题”
已知实数x，y满足：x2+3y2﹣3=0，求x+y的取值范围．
解：已知等式x2+3y2﹣3=0可化为：=1，
此为椭圆方程，故由椭圆的参数方程可知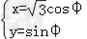（φ为参数）
所以x+y=，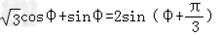
故由三角函数的性质，可知x+y的取值范围为[﹣2，2]．
