已知曲线C上任意一点P到两定点F1(-1,0)与F2(1,0)的距离之和为4.
(1)求曲线C的方程;
(2)设曲线C与x轴负半轴交点为A,过点M(-4,0)作斜率为k的直线l交曲线C于B、C两点(B在M、C之间),N为BC中点.
(ⅰ)证明:k·kON为定值;
(ⅱ)是否存在实数k,使得F1N⊥AC?如果存在,求直线l的方程,如果不存在,请说明理由.
(1)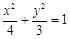 ;(2)(ⅰ)
;(2)(ⅰ)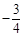 ;(ⅱ)不存在.
;(ⅱ)不存在.
题目分析:(1)由于曲线C上任意一点P到两定点F1(-1,0)与F2(1,0)的距离之和为4,结合椭圆的定义可知曲线C是以两定点F1(-1,0)和F2(1,0)为焦点,长轴长为4的椭圆,从而可写出曲线C的方程;
(2)由已知可设出过点直线l的方程,并设出直线l与曲线C所有交点的坐标;然后联立直线方程与曲线C的方程,消去y就可获得一个关于x的一元二次方程,应用韦达定理就可写出两交点模坐标的和与积;(ⅰ)应用上述结果就可以用k的代数式表示出弦的中点坐标,这样就可求出ON的斜率,再乘以k就可证明k·kON为定值;(ⅱ)由F1N⊥AC,得kAC•kFN= -1,结合前边结果就可将此等式转化为关于k的一个方程,解此方程,若无解,则对应直线不存在,若有解,则存在且对应直线方程很易写出来.
试题解析:(1)由已知可得:曲线C是以两定点F1(-1,0)和F2(1,0)为焦点,长轴长为4的椭圆,所以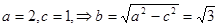 ,故曲线C的方程为:
,故曲线C的方程为: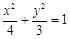 . 4分
. 4分
(2)设过点M的直线l的方程为y=k(x+4),设B(x1, y1),C(x2, y2)(x2>y2).
(ⅰ)联立方程组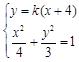 ,得
,得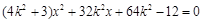 ,
,
则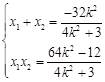 , 5分
, 5分
故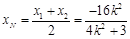 ,
,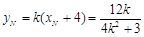 , 7分
, 7分
所以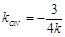 ,所以k•kON=
,所以k•kON=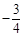 为定值. 8分
为定值. 8分
(ⅱ)若F1N⊥AC,则kAC•kFN= -1,
因为F1 (-1,0),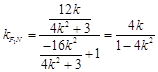 故
故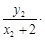
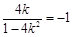 , 10分
, 10分
代入y2=k(x2+4)得x2=-2-8k2,y2="2k" -8k3,而x2≥-2,故只能k=0,显然不成立,所以这样的直线不存在. 13分
