问题
解答题
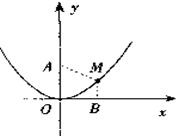
已知一条曲线在x轴的上方,它上面的每一点到点A(0,2)的距离减去它到x轴的距离的差都是2,求这条曲线的方程.
答案
设点M(x,y)是曲线上任意一点,MB⊥x轴,垂足是B,那么点M属于集合P={M||MA|-|MB|=2}.
由距离公式,点M适合的条件可表示为:
-y=2①x2+(y-2)2
将①式移项后再两边平方,得x2+(y-2)2=(y+2)2,
化简得:y=
x21 8
因为曲线在x轴的上方,所以y>0,虽然原点O的坐标(0,0)是这个方程的解,但不属于已知曲线,所以曲线的方程是y=
x2(x≠0),它的图形是关于y轴对称的抛物线,但不包括抛物线的顶点,如图所示.1 8