问题
解答题
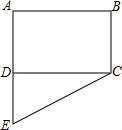
已知:矩形ABCD的面积为12,边AB与BC的长是关于x的方程x2-(m-5)x+m=0的两个根.
(1)分别求出边AB和BC的长度;
(2)以点A为圆心,AB长为半径画弧,交射线AD于点E,求四边形ABCE的面积.
答案
(1)∵边AB与BC的长是关于x的方程x2-(m-5)x+m=0的两个根,
∴AB+BC=m-5,AB•BC=m,
又∵AB•BC=12,
∴m=12,
∴AB=3,BC=4,或AB=4,BC=3;
(2)∵AE∥BC,AE≠BC,
∴AB与CE不平行,即四边形ABCE是梯形.
当AB=3,BC=4时,S=
(3+4)×3=1 2
,21 2
当AB=4,BC=3时,S=
(3+4)×4=14,1 2
综上所述,四边形ABCE的面积为
或14.21 2