问题
填空题
经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点，并且圆心在直线x-y-4=0上的圆的方程 ．
答案
题目分析：设经过两圆交点的圆的方程为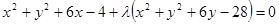
,整理为
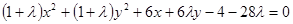,再整理：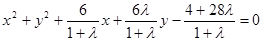
.
圆心坐标为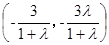
，代入直线方程，解得：
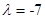，代入得圆的方程：
.
搜题请搜索小程序“爱下问搜题”
经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点，并且圆心在直线x-y-4=0上的圆的方程 ．
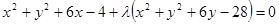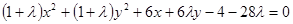题目分析：设经过两圆交点的圆的方程为,整理为,再整理：.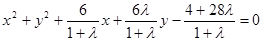
圆心坐标为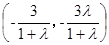，代入直线方程，解得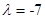：，代入得圆的方程：
.