问题
解答题
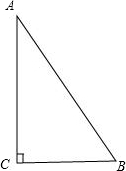
在△ABC,∠C=90°,斜边AB=10,直角边AC、BC的长是关于x的方程x2-mx+3m+6=0的两个实数根.
(1)求m的值;
(2)计算sinA+sinB+sinA•sinB.
答案
(1)如图,设AC=x1,BC=x2,
由题意,得
x1+x2=m>0,x1x2=3m+6>0.
在Rt△ABC中,AC2+BC2=100,
即x12+x22=100,
(x1+x2)2-2x1x2=100.
m2-6m-112=0.
解得m1=14,m2=-8(舍去).
∴m=14.
(2)sinA+sinB+sinAsinB=
+x2 10
+x1 10
×x2 10 x1 10
=
+x1+x2 10 x1x2 100
由x1+x2=m=14,x1x2=3m+6=3×14+6=48得:
+x1+x2 10
=x1x2 100
+14 10
=48 100
.47 25