问题
填空题
在平面直角坐标系xOy中,设点P(x1,y1)、Q(x2,y2),定义:d(P,Q)=|x1-x2|+|y1-y2|.已知点B(1,0),点M为直线x-2y+2=0上的动点,则使d(B,M)取最小值时点M的坐标是______.
答案
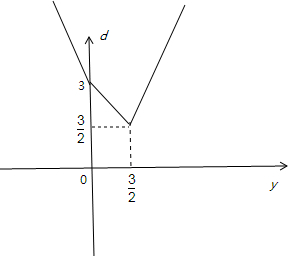
设M(2y-2,y),由题意d(B,M)=|2y-2-1|+|y-0|=|2y-3|+|y|=
,-3y+3y<0 3-y0≤y< 3 2 3y-3y≥ 3 2
显然y=
时d(B,M)取最小值,此时M(1,3 2
)3 2
故答案为:(1,
)3 2