问题
解答题
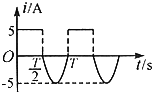
已知点A（3，3）、B（5，2）到直线l的距离相等，且直线l经过两直线l1：3x-y-1=0和l2：x+y-3=0的交点，求直线l的方程．
答案
解方程组
得交点P（1，2）．3x-y-1=0 x+y-3=0
（1）若A、B在直线L的同侧，则L∥AB，
KAB=
=-3-2 3-5
，1 2
∴直线的方程是：y-2=-
（x-1），1 2
即x+2y-5=0．
（2）若A、B分别在直线L的异侧，则直线L过线段AB的中点（4，
），5 2
∴直线L的两点式方程是
=y-2 x-1
，
-25 2 4-1
即x-6y+11=0．
综（1）（2）知直线L的方程是x+2y-5=0或x-6y+11=0．