问题
解答题
从2开始，连续的偶数相加，它们的和的情况如下表：
加数m的个数 和(S)
1 ———————————→2＝1×2
2 ————————→2＋4＝6＝2×3
3 ——————→2＋4＋6＝12＝3×4
4 ————→2＋4＋6＋8＝20＝4×5
5 ——→2＋4＋6＋8＋10＝30＝5×6
(1)按这个规律，当m＝6时，和为_______；
(2)从2开始，m个连续偶数相加，它们的和S与m之间的关系，用公式表示出来为：
__________________________________________．
(3)应用上述公式计算：
①2＋4＋6＋…＋200 ②202＋204＋206＋…＋300
答案
（1)__42__；
(2)___s=m(m+1)__；
(3)应用上述公式计算：
①2＋4＋6＋…＋200
=100
101
=10100
②202＋204＋206＋…＋300
=2+4+6+…+300-10100
=150151-10100
=12550
（1）由表中的式子可得S与n之间的关系为：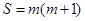
；
（2）首先确定有几个加数，由上述可得规律：加数的个数为最后一个加数÷2，据此解答．