问题
解答题
已知线段PQ两端点的坐标分别为(-1,1)、(2,2),若直线l:x+my+m=0与线段PQ有交点,求m的取值范围.
答案
[-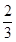 ,
,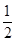 ]
]
解法一:直线x+my+m=0恒过点A(0,-1),
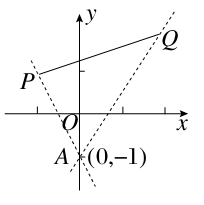
kAP=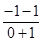 =-2,kAQ=
=-2,kAQ=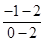 =
=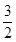 ,
,
则-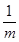 ≥
≥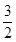 或-
或-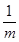 ≤-2.
≤-2.
∴-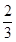 ≤m≤
≤m≤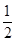 且m≠0.
且m≠0.
又m=0时,直线x+my+m=0与线段PQ有交点,
∴所求m的取值范围是[-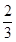 ,
,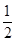 ].
].
解法二:过P、Q两点的直线方程为y-1=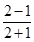 (x+1),
(x+1),
即y=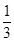 x+
x+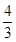 ,代入x+my+m=0,整理
,代入x+my+m=0,整理
得x=-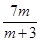 ,
,
由已知-1≤-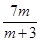 ≤2,解得-
≤2,解得-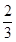 ≤m≤
≤m≤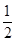 .
.
即m的取值范围是[-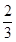 ,
,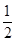 ].
].
