(1)定点(－2，1); (2) x－2y＋4＝0.

题目分析：(1)由直线系方程: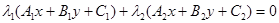 恒过两直线: 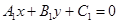与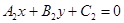的交点可知:只需将直线L的方程改写成: 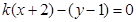知直线L恒过直线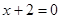与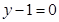的交点(-2,1),从而问题得证;(2)先用k将点A和点B的坐标表示出来，由直线L交x轴负半轴于点A，交y正半轴于点B知：k>0;然后再用含k的代数式将△AOB的面积为S表达出来，得到S是k的函数，再利用基本不等式就可求得使S取得最小值对应的k的值，从而就可写出直线L的方程.

试题解析：(1)证明：由已知得: k(x＋2)＋(1－y)＝0，        3分

令   x＋2="0" ， 1－y=0

得: x=-2 ， y=1

∴无论k取何值，直线过定点(－2，1)     5分

(2)解：令y＝0得：A点坐标为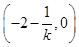

令x＝0得：B点坐标为(0，2k＋1)(k>0)，      7分

∴S_△AOB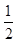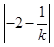＝ |2k＋1|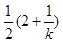＝ (2k＋1)

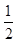＝≥ (4＋4)＝4      .10分

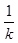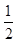当且仅当4k＝，即k＝时取等号．

即△AOB的面积的最小值为4，此时直线l的方程为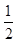x－y＋1＋1＝0，

即 x－2y＋4＝0.                           12分