问题
解答题
已知复数z满足|z＋2－2i|＝1，求|z－3－2i|的最大值\与最小值．
答案
4，6
由复数及其模的几何意义知：满足|z＋2－2i|＝1，即|z－(－2＋2i)|＝1.
复数z所对应的点是以C(－2,2)为圆心，r＝1为半径的圆．而|z－3－2i|＝|z－(3＋2i)|的几何意义是：复数z对应的点与点A(3,2)的距离．由圆的知识可知|z－3－2i|的最小值为|AC|－r，最大值为|AC|＋r.
∴|z－3－2i|min＝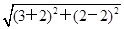
－1＝4.
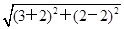|z－3－2i|max＝＋1＝6.
