问题
证明题
对于任意空间四边形，试证明它的一组对边中点的连线与另一组对边可平行于同一平面．
答案
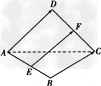
证明：如图所示，空间四边形ABCD ，E 、F 分别为AB 、CD 的中点，利用多边形加法法则可得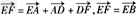
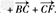①
又E、F分别是AB、CD的中点，
故有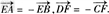
②
将②代入①后，两式相加得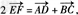
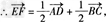
即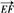
与
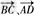共面，
∴EF与AD、BC可平行于同一平面．
搜题请搜索小程序“爱下问搜题”
对于任意空间四边形，试证明它的一组对边中点的连线与另一组对边可平行于同一平面．
证明：如图所示，空间四边形ABCD ，E 、F 分别为AB 、CD 的中点，利用多边形加法法则可得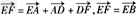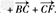①
又E、F分别是AB、CD的中点，
故有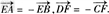②
将②代入①后，两式相加得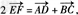
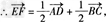
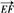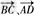即与共面，
∴EF与AD、BC可平行于同一平面．