问题
选择题
在正三棱柱ABC—A1B1C1中，D是AC的中点，AB1⊥BC1，则平面DBC1与平面CBC1所成的角为( )
A．30°
B．45°
C．60°
D．90°
答案
答案：B
以A为坐标原点，
，
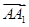的方向分别为y轴和z轴的正方向建立空间直角坐标系．
设底面边长为2a，侧棱长为2b，
则A(0,0,0)，C(0,2a,0)，D(0，a,0)，B(
a，a,0)，C1(0,2a,2b)，B1(a，a,2b)．
由
⊥
，得·＝0，即2b2＝a2.
设n1＝(x，y，z)为平面DBC1的一个法向量，
则n1·
＝0，n1·
＝0.
即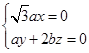
又2b2＝a2，令z＝1，
解得n1＝(0，－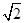
，1)．
同理可求得平面CBC1的一个法向量为n2＝(1，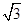
，0)．
利用公式cos θ＝
＝
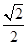，得θ＝45°.