某商店准备从机械厂购进甲、乙两种零件进行销售，若每个甲零件的进价比每个乙种零件的进价少2元，且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同。
（1）求甲、乙两种零件每个的进价分别为多少元？
（2）若该商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个，购进两种零件的总数量不超过95个，将本次购进的甲、乙两种零件全部售出后，可使销售两种零件的销售价格均为12元，则将本次购进的甲、乙两种全部售出后，可使销售两种零件的总利润（利润=售价－进价）超过302元，通过计算求出该商店本次从机械厂购进甲、乙两种零件有几种方案？请你设计出来。
（1）甲种零件进价为8元，乙种零件进价为10元（2）方案一，购进甲种零件67个，乙种零件24个；方案二：购进甲种零件70个，乙种零件25个
（1）设每个乙种零件进价为x元，则每个甲种零件进价为（x-2）元，
依题意得
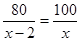解得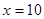
…………2分
经检验x=10是方程的解，10-2=8 …………3分
答：甲种零件进价为8元，乙种零件进价为10元 …………4分
（2）设购进乙种零件为y个，则购进甲种零件（3y-5）个，依题意得
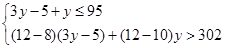…………6分
解得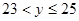
…………8分
∵y为整数 ∴y=24或25 ∴共2种方案
分别是：方案一，购进甲种零件67个，乙种零件24个；
方案二：购进甲种零件70个，乙种零件25个. ………10分
（1）设每件乙种商品的进价为x元，则每件甲种商品的进价为（x-2）元，根据题意建立方程求出其解就可以了．
（2）本题中“根据进两种商品的总数量不超过95个”可得出关于数量的不等式，根据“使销售两种商品的总利润（利润=售价-进价）超过302元”可以得出关于利润的不等式，组成不等式组后得出未知数的取值范围，然后根据取值的不同情况，列出不同的方案．