问题
解答题
若e1、e2、e3是三个不共面向量，则向量a=3e1+2e2+e3，b=-e1+e2+3e3，c=2e1-e2-4e3是否共面？请说明理由．
答案
解：设c=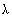
1a+
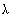2b，
则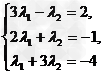
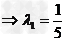
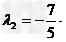
即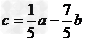
∵a、b不共线，
向量a、b、c共面．
搜题请搜索小程序“爱下问搜题”
若e1、e2、e3是三个不共面向量，则向量a=3e1+2e2+e3，b=-e1+e2+3e3，c=2e1-e2-4e3是否共面？请说明理由．
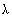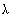解：设c=1a+2b，
则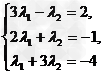
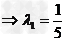
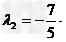
即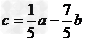
∵a、b不共线，
向量a、b、c共面．