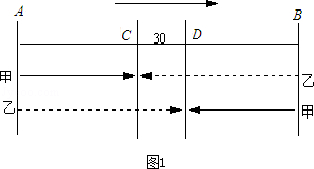
A、B两个港口相距300公里.若甲船顺水自A驶向B,乙船同时自B 逆水驶向A,两船在C处相遇.若乙船顺水自A驶向B,甲船同时自B逆水驶向A,则两船于D 处相遇,C、D相距30公里.已知甲船速度为27公里/小时,则乙船速度是 公里/小时.
33或22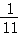
题目分析:两次相遇所用的时间相等.
若C在D的上游,则根据乙比甲多走30公里列出方程解答即可;
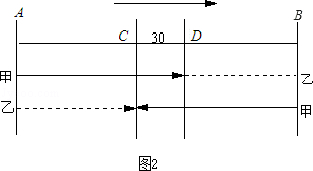
若C在D的下游,则根据甲比乙多走30公里列出方程解答即可.
解:已知A、B两港相距300公里,甲船速为27公里/小时.设乙船速为v公里/小时,水流速为x公里/小时,则甲船顺水速为(27+x)公里/小时,逆水速为(27﹣x)公里/小时.乙船顺水速为(v+x)公里/小时,逆水速为(v﹣x)公里/小时.
甲船自A顺水,乙船自B逆水同时相向而行,相遇在C处时间为: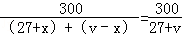
同理,乙船自A顺水,甲船自B逆水同时相向而行,相遇在D处所需时间为: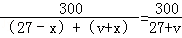
可见,两个时间相等.由图易见,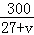 小时中,乙船比甲船多走30公里,即:
小时中,乙船比甲船多走30公里,即:
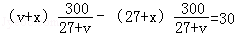 ,
,
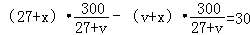 ,
,
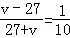 ,
,
v=33.
如果C在D的右边,由图易见,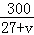 小时中,甲船比乙船多走30公里,即:
小时中,甲船比乙船多走30公里,即:
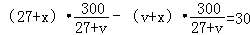 ,v=22
,v=22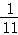 .
.
答:若C在D的左边,乙船速度是33公里/小时;若C在D的右边,乙船速度是22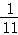 公里/小时.
公里/小时.
故答案为33或22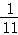 .
.
点评:考查分式方程的应用;根据在相同时间内两船所走路程相差30公里得到等量关系是解决本题的关键.
