问题
计算题
如图1所示，质量M=1.0kg的木板B静止放在水平地面上，质量m= 0.5kg的电动玩具小车A位于木板的左端．小车从静止启动后匀加速地向木板右端驶去，小车对木板的作用力使木板也同时开始运动，取小车A的运动方向为正方向，小车A和木板B的v-t图象如图2所示．经过t=0.6s时小车与挡板相碰，碰后两者立刻粘合在一起运动，且碰后小车电动机的电源被切断．g=10m/s2，求：
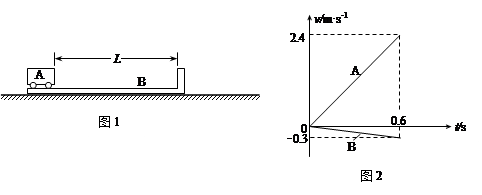
（1）开始时小车A与木板右端挡板的距离L．
（2）木板与地面间的动摩擦因数μ．
（3）从小车启动到最终木板停下全过程，木板的总位移sB．
答案
（1）0.81m （2）0.1（3）0.09m 向右
题目分析：（1）t=0.6s时小车A和木板B的速度大小分别为vA=2.4m/s、vB=0.3m/s．
开始时小车A与木板右端挡板的距离
①
代入数据解得L=0.81m ②
（2）小车A在木板上运动过程，受木板的作用力
③
木板受力向左加速运动，有
④
F’ = F ⑤
小车A和木板B的加速度大小分别为
⑥
⑦
代入数据解得木板与地面间的动摩擦因数
μ=0.1 ⑧
（3）小车与挡板碰后立刻粘合，动量守恒，有
mυA – MυB =" (m" + M)υ ⑨
碰后滑行过程，由动能定理得
μ (m + M)gs’ =
(m + M)υ2 ⑩
代入数据，解得碰后位移
s’ =" 0.18m" （向右）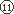 
而木板碰前的位移
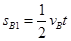=0.09m（向左） 
因此木板的总位移
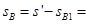0.09m（向右） 
