解：三垂线定理：在平面内的一直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。

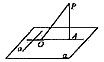
已知：如图，PA、PO分别是平面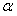的垂线、斜线，AO是PO在平面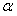内的射影， 且a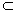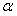，a⊥AO。

求证：a⊥PO。

证明：∵P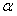A⊥，a，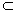

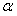∴PA⊥a，

又AO⊥a，且PA与AO平面PAO内两条相交直线，

∴a⊥平面PAO，而PO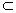平面PAO，

∴a⊥PO。