问题
解答题
P是△ABC所在平面外一点,A′、B′、C′分别是△PBC、△PCA、△PAB的重心,
(1)求证:平面A′B′C′∥平面ABC;
(2)求S△A′B′C′:S△ABC.
答案
证明:(1)如图,分别取AB,BC,CA的中点M,N,Q,
连接PM,PN,PQ,MN,NQ,QM,
∵A′,B′,C′分别是△PBC、△PCA、△PAB的重心,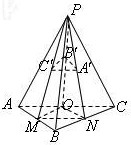
∴A′,B′,C′分别在PN,PQ,PM上,
且PC′:PM=PA:PN=PB:PQ=2:3.
在△PMN中,
=PC′ PM
=PA′ PN
,2 3
故C′A′∥MN,
又M,N为△ABC的边AB,BC的中点,MN∥AC,
∴A′C′∥AC,
∴A′C′∥平面ABC,
同理A′B′∥平面ABC,
∴平面ABC∥平面A′B′C′;
(2)由(1)知,
=A′B′ QN
,2 3
=QN AB
,1 2
∴A′B′:AB=1:3.
∴S△A′B′C′:S△ABC=(A′B′)2:(AB)2=1:9.
